Connecting the four operations
I often say to primary age children that there are only five things they can do to a number. One of those is to leave it alone! So, the fact that there are only four operations – four things you can do to a number as a primary student – comes as a relief to some who are drowning in what feels like a sea of infinite and unconnected processes.
It is a eureka moment when they realise that all they can be asked to do is add to a number, subtract from it, multiply or divide it. Everything they learn about number can be reduced to one of these four operations.
Helping children to establish in their minds the differences between the four operations and the connections between them is a work which spans the primary years. Without a doubt, it should be an area which we revisit often.
Classroom resource
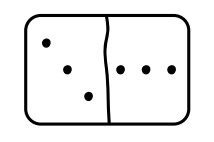
The downloadable worksheet may be useful for revisiting this area. The resource shows a simple domino-type image of doubles. It invites children to write equations about what they can see using all four operations.
Provoke discussion
The worksheet (or should we call it a talksheet?) will push children’s thinking and provoke useful discussion. The questions are endless….
What can you see? How many dots on the left? How many on the right? How many dots altogether? What does altogether mean, because the dots are clearly not “altogether”? Can you see two groups? If so, where are the groups because I can’t see any groups? How could we write about what we can see in full sentences? What mathematical symbol can we use? How else can we write about what we can see? What other symbols could we use? What if the dots used to be together and now they have been pulled apart? How would you write about it then? What is an inverse operation?
If you worked through these discussions with your class, you would be exposing underlying structures and making connections in a rich way.
If you followed this up by giving your class one of these images every day for a week, you would notice a difference not just in the speed with which they churn out equations using all four operations, but the way in which they talk about the links between the four operations. Like all good ideas, it is the simplicity of this exercise which makes it powerful.